数控机床的故障分布模型和可靠性评价技术研究
数控机床最重要的3个指标为精度、效率和可靠性。国家非常重视机床的可靠性问题,在“高档数控机床与基础制造装备”科技重大专项中投入了大量资金用于机床可靠性的研究和提升。在2009年和2010年的机床重大专项中,机床及功能部件的可靠性相关项目共计13个,其中沈阳机床参与承担了6个。通过参与承担国家重大专项,大大提升了企业的可靠性技术实力和机床的可靠性水平。
作者将对机床的故障数据进行统计整理,在此基础上进行参数估计和拟合校验得到数控机床的数学期望值,并进行可靠性综合评价,从而更全面和准确地评价机床的可靠性水平。
因为故障数据的分布类型尚不确定,因此应该先对其进行估计。将表1中的数据分成k组,k根据式(1)确定:
对分布函数进行对数正态分布、威布尔分布、正态分布、指数分布和瑞利分布的参数估计和拟合校验。其中参数分布采用极大似然法,由于篇幅有限,不再给出理论过程。拟合校验采用k-s法,得到各种分布的校验值,如表2所示。
其中:H表示是否符合假设分布,0表示不符合,1表示符合;P表示服从分布的概率大小,某一分布的P值越大,数据符合该分布可能性越大。由表2可以看出,故障数据符合威布尔分布。在Matlab环境下基于极大似然法得到的威布尔分布参数估计值为1.482和1.274,威布尔分布时的数学期望值(MTBF)为1374.9h。
为了消除指标量纲的影响,采用TOPSIS方法对评价指标进行量纲为一的标准化处理。
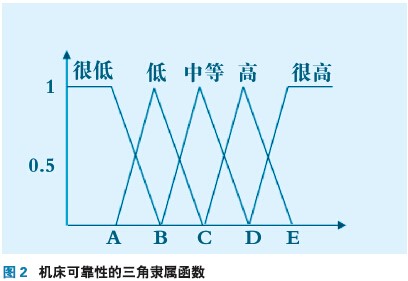
采用模糊理论对机床的可靠性进行模糊评价,建立机床的三角隶属度函数图,如图2所示。
由此可以得到数控机床的评价集合:
机床的可靠性技术包括可靠性设计、可靠性试验、可靠性增长和可靠性评价等内容。可靠性评价技术对了解机床的可靠性水平具有重要的现实意义。国内外学者在此方面做了很多工作,如乔巍巍对数控系统进行了可靠性建模和可靠性综合技术的研究,张宏斌等采用模糊评价方法对电火花线切割机床进行了可靠性评估,张忠松对加工中心的可靠性评价指标和方法进行了分析,贾志成等分析了协同环境下的加工中心寿命和可靠性评估。
1 故障数据的参数估计和拟合校验
表1所示是收集的一组某数控机床的故障数据(MTBF值)。

其中,n为数据个数。
每一组的概率密度值可以由式(2)确定。
其中:ni为每一区间的数据个数;b为区间宽度。
在Matlab环境下采用极大似然法对故障数据进行概率密度函数拟合,其概率密度拟合图如图1 所示。


2 可靠性综合评价
对于数控机床的可靠性评价,单项指标(如MTBF)仅能代表机床某一方面的信息,其他如平均维修时间(MTTR)和首次故障时间(MTTFF)尚没有考虑在内。对这些参数进行综合分析,可以系统全面地评价机床的可靠性水平。在评价中,对指标合理分配权重是量化估计的关键,基于专家经验并融合信息熵理论确定机床各指标的综合权重。模糊综合评价方法应用模糊理论,从多因素角度对机床各指标的隶属等级进行综合评价,结果更为客观和深入。
由于篇幅有限,这里直接给出数控机床的MTTR和MTTFF值,分别为28.6和1002h。
将热力学中的熵理论引入可靠性评价中,机床可能处于不同的可靠性状态,每种状态出现的概率为Pi(i=1,2,3,…,m)。系统的熵定义为
式中:m为待评的状态数,n为评价指标,则由数控机床可靠性数学期望值可以构成一个m×n 阶的矩阵。
对于某个指标rj,有信息熵:
第j 个指标的熵权定义为:
这样可以得到基于信息熵的评价指标权重向量:
熵值越小表明指标值的变异程度越大,在综合评价中所起的作用也越大,其权重也应该越大;反之亦然。
根据以上分析,数控机床的评价指标可以设定为:
D=(MTBF,MTTR,MTTFF)
文中考核的是一种型号的机床,即m=1,用n表示3个评价指标,则原始数据是一个1×3阶的矩阵,即
D=(1374.9,28.6,1002)
根据国家科技重大专项和专家经验确定各项指标的阈值,将各可靠性评价指标分为5个评判等级,如表3所示。

为了避免人为对某些指标赋予的权重过高或过低,采用专家经验和信息熵值结合的方法,确定指标综合权重。熵的计算依据式(6),经过咨询多位专家的意见,专家评价各指标的权重向量为
E=(0.5,0.35,0.15)
因此,结合专家经验和信息熵值的综合权重为
式中:wjH为信息熵权值;ej为专家经验权值。由此,可得到数控机床的综合权重向量:
W=[0.166 7,0.117,0.05]
综合评价的结果可以由RE=W·R 得到,计算结果为
RE=[0,0,0.1395,0.7133,0.1472]
数控机床可靠性综合评价的流程如图3所示。

3 结束语
在对数控机床的故障数据进行整理分析的基础上,通过对其参数估计和拟合校验得到了威布尔分布时数控机床的数学期望值。鉴于数控机床可靠性的模糊性,采用模糊理论评价数控机床的可靠性,并通过融合信息熵理论和专家知识确定各指标的综合权重,为数控机床的可靠性评价提供了一种高可信性和高精度的方法。
另外,从数控机床可靠性综合评价的结果也可以看出,所分析数控机床的可靠性较高,说明了“高档数控机床与基础制造装备”科技重大专项实施的重要性和企业在机床可靠性工作方面的有效性。
 销售热线:188 2384 2885
销售热线:188 2384 2885





