基于敏感度分析的机床关键性几何误差源识别方法新算法

---

0 前言

随着航空航天、军工、船舶、汽车等行业对精密零件加工的要求越来越高，机床的精度性能显得更加重要，精密数控机床的设计制造也以高精度、高智能化、高效率为主要目标。精度设计是保证和提高机床精度的重要一环，传统的机床设计中，主要依靠经验的方法设计机床各部件的公差等级。由于各环节误差对机床整体精度的影响程度不同，精度控制实现的难易程度也不同。因此，为节约机床的设计及制造成本，分析影响机床加工精度的各主要因素，建立机床的精度模型并进行误差敏感度分析显得尤其重要。精度设计对精密数控机床的设计与制造具有重要的实际应用意义。

影响机床整体加工精度的各类误差主要有机床零部件的几何误差、热误差、载荷误差、伺服误差和插补误差等，而几何误差对加工精度的影响又是精度设计的主要研究内容。机床的综合几何误差体现在各零部件上，最终均将反映在被加工工件的加工误差上，而通过准确建立机床的精度模型，可以反映出整体精度与各零部件的精度关系。国内外许多学者对数控机床空间误差建模方法进行了较广泛而深入的研究，先后出现了几何建模法、误差矩阵法、二次关系模型法、机构学建模法、刚体运动学法和多体系统理论法等。多体系统是一般机械系统最为全面的完整抽象、高度概括和有效描述，是分析和研究机械系统的最优模型形式。目前国内外众多学者已应用多体系统理论对机床进行精度建模与分析。POTT等通过一种基于简化矢力的方法分析了并联机构运动灵敏度，并通过分析6自由度并联机构Linapod，验证了方法的正确性。王冰采用综合误差敏感度、绝对误差敏感度和误差方向敏感度这三个误差评价指标，将各个机床误差影响因素对机床终端误差的影响进行了分析。李小雷等对刻楦机进行了误差参数灵敏度分析。程刚等针对以3-RPS并联机构可达空间内各误差来源，提出了一种通过归一化描述灵敏度的新方法，并建立基于数学统计意义的灵敏度系数数学模型。黄强等以滚齿机YK3610为对象，介绍基于多体系统理论和齐次坐标变换的机床误差建模方法，并对机床敏感误差辨识方法、步骤和关键点进行阐述。但是，通过分析可以看出，目前针对机床误差进行敏感度分析的文献还较少，对机床误差溯源的研究深度不够。

本文是在国家重大科技专项“精密立、卧式加工中心研究”和国家自然科学基金项目“基于模糊稳健设计的机床动态精度分析与反演方法研究”的课题背景下，对精密加工中心进行精度设计。为了有效地识别出对机床加工精度及空间误差影响较大的几何误差参数，首先基于多体系统理论的方法，分析各部件几何误差对机床精度的影响，建立精密卧式加工中心的精度模型；然后提出了基于矩阵微分法的四轴机床误差敏感度分析数学方法，根据模型计算精密卧式加工中心的误差敏感度和敏感度系数，从而进行误差溯源。

1 基于多体系统理论的精度建模

根据精密卧式加工中心的结构与运动特点，将机床抽象成多体系统，用拓扑结构和低序体阵列描述机床各部分的关联性；在多体系统中建立广义坐标系，用齐次变换矩阵把机床各部件的误差量之间的耦合关系表述出来；推导出机床中两相邻体之间相对运动的特征矩阵和运动方程，从而建立加工中心的精度模型。

1.1 广义坐标系的设置及机床的特征矩阵

精密卧式加工中心是一台四轴数控机床，具有高刚度、高精度、高速度的特点，根据设计要求，其技术指标如表1所示，其刀柄型号为BT50。

加工中心的结构简图如图1所示，它由床身，X、Y、Z三轴运动部件，主轴箱（刀具）和绕B轴旋转的工作台组成。

根据多体系统理论的方法，将机床各组成部件分成相应的“体”。并按床身—X轴运动部件—Y轴运动部件—主轴箱（刀具）分支，和床身—Z轴运动部件—工作台—工件分支分别对其编号，图2为机床的拓扑结构，表2是其低序体阵列，表2中Ln（j）是体Bj的n阶低序体阵。

一般来说，机床的每一个单元部件在处于静止或运动状态时都存在空间6个自由度方向的基本误差，通过分析精密卧式加工中心的结构及其运动关系可知，加上工件的装夹误差，其中影响机床加工精度的几何误差主要有35项，这部分几何误差在机床总误差中占了较大的比重，表3列出了机床各部件的几何误差（部分）。

多体系统中各体之间的位置和运动关系可以用相应的坐标系的位姿变换来表示，为了方便机床的精度建模，需要对坐标系进行特殊设置处理。设置如下：①在床身（B0）和所有运动部件（Bj）上均建立起与其固定联接的右手笛卡儿三维坐标系，这些坐标系的集合成为广义坐标系（又称参考坐标系），各体坐标系称为子坐标系（又称动坐标系）。每个坐标系的3个正交基按右手定则分别为Xj、Yj、Zj轴；②广义坐标系各元素Xj、Yj、Zj轴分别对应平行；③X轴部件、Y轴部件（主轴箱）、Z轴部件、工作台的体运动参考系与其对应相邻低序体的体坐标系重合；④刀具坐标系原点与主轴端面中心重合；⑤工件上设定工件坐标系。

根据加工中心的结构和各部件之间的运动关系，可建立各相邻体间的变换特征矩阵。考虑到加工中心运动部件的一些静止误差或者非运动部件的运动误差相对很小，可令其误差特征矩阵为单阵I4×4。表4为精密卧式加工中心各部件的特征矩阵T。

表4中带下标p的量表示静止状态特征矩阵，带下标s的量表示运动状态的特征矩阵。

式中，x、y、z分别为X轴部件、Y轴部件、Z轴部件的位移，α、β、γ分别为轴X、Y、Z的相位角。

1.2机床精度模型

设刀具成形点在刀具坐标系内的坐标为

工件上成形点在工件坐标系中的坐标为

理想运动条件下有
式中

那么，机床在无误差情况（理想情况）下，刀具成形点在工件坐标系内的理想成形函数为

在机械加工中，机床加工精度最终是由机床上刀具成形点与工件成形点之间的相对位移误差决定的。在实际加工过程中，刀具成型点的实际位置不可避免地会偏离理想位置，从而产生空间位置误差。实际成形点与理想刀具成形点的综合空间位置误差为

式中E——机床的空间误差矢量

Ex,Ey,Ez——X轴、Y轴、Z轴方向上的误差式（5）就是精密卧式加工中心的综合精度模型，它由机床各部件的几何误差组成，根据此精度模型，基于敏感度分析可以识别对机床加工精度具有重要影响的关键性误差源。

2关键误差源识别

根据精密卧式加工中心的精度模型，利用矩阵微分法建立四轴机床误差敏感度分析的数学模型。通过计算各个部件单元几何误差的敏感度，比较各个误差元素对总的空间误差的影响程度，最终识别出了影响机床加工精度的关键性误差源，从而为合理经济地提高机床的精度提供重要的理论依据。

2.1机床空间误差敏感度分析模型的建立

根据式（5），可以建立一般的四轴数控机床的误差计算模型，该模型可以显性地表示为

式中G——n个机床各零部件几何误差组成的误差矢量
G=（△ei,△e2,...,△en）T
△ei——机床部件的几何误差，i=1,2,...
Pw——工件上成形点在工件坐标系中的坐标矢量
Pw=（pwxpwypwz1）T
U——机床各运动轴的位置矢量
U=（x,y,z,B）T
Uw——工件位置坐标矢量
Uw=（xw,ywzw,1）T
Ut——刀具位置坐标矢量
Ut=（xt,ytt,zt1）T
根据式（5）的形式，可知F是变量G、Pw、U、Uw、Ut的连续可微函数，因此式（6）按一阶泰勒级数展开，可以表达为

式中，ΔG、ΔPw、ΔU、ΔUw、ΔUt分别为G、Pw、U、Uw、Ut在其理想值处的微小波动量，去掉高阶项，可以得到

在实际的分析过程中，Pw、U、Uw、Ut可设为定值，即在固定的工件、刀具安装位置下，模拟加工相同的工件轨迹，分析由机床各部件的几何误差变化时对总的空间误差影响程度的大小。因此式（8）简化为

进而可以得到机床加工精度的敏感度分析模型为

式中，S=δF/δG为雅可比矩阵，称为误差敏感度矩阵，并具有如下的形式

至此，用矩阵微分的方法，得到了一般四轴数控机床的误差敏感度矩阵的表达式。

2.2零部件几何误差参数的检定

本论文以图1所示的精密卧式加工中心为研究对象，以图3为检验加工对象，利用QC20-W球杆仪和APIXD-6D双频激光干涉仪对各几何误差进行测试检定，如图4所示。测得精密卧式加工中心的35项几何误差，考虑到篇幅有限，表5仅列出了部分几何误差值。

将表5所示的检测几何误差以及工件的安装位置（xwd,ywd,zwd,1）T、刀具的安装位置（xtd,ytd,ztd,1）T、各导轨的运动位移x、y、z代入到式（5），就可以得到工件上每个加工位置（pwx,pwy,pwz,1）T的误差。根据精密加工中心的几何精度检验标准GB/T20957.7—2007《精密加工中心检验条件第7部分：精加工试件精度检验》，将加工试件安装在工作台中心，在x-y平面上切削一个直径d=218mm的圆，如图3所示。

在机床的工作空间区域中，各坐标轴处于中间位置的工作区域使用最频繁，因此主要对机床中间工作区域进行误差敏感度的分析。根据精密卧式加工中心的设计结构、技术参数以及多体系统中广义坐标系的设置，可设定工件坐标系原点在工作台坐标系中的位置坐标为
（xwdywdzwd1）T=（500-1901181）T
刀具坐标系原点在主轴坐标系中的坐标为
（xtdytdztd1）T=（00-1901）T
工件上加工点的坐标取值范围是
pwx=[-109,109]pwy=[553.5,771.5]pwz=-150
各个运动轴的取值范围是
x=[391,609]y=[363.5,581.5]z=118
工作台转角b=0并且有
pwx=x-500pwy=y+190
其中，根据典型试件加工轨迹的特点，可得x、y的关系为
（x-500）2+（y-472.5）2=1092
本文中，取机床加工试件时运动到最高点（x，y，z）=（500,581.5,118）的位置对机床进行误差
敏感度分析（以上各参数值的单位为mm）。

2.3关键性误差源参数的识别

机床的加工精度受到零部件几何误差耦合而成的空间误差的影响，每一项误差对综合加工精度影响程度大小不一样，究竟哪些空间几何误差参数对机床总加工精度的影响较大，主要影响着机床的加工精度，为了找出各个误差元素对总的空间误差的影响程度大小，需要对机床的精度模型进行误差敏感度分析。针对本文分析的精密卧式加工中心，其精度模型包含了机床各个运动部件产生的几何误差共35项。

误差敏感度反映的是各个误差元素产生微小变化时总空间误差的变化程度，根据式（5）的精度模型和式（11）的误差敏感度矩阵，可以定义机床的空间误差E对各个几何误差Δei的偏导数的绝对值为精密卧式加工中心的误差敏感度

对于的误差敏感度S△γz，由式（5）、（11），可得

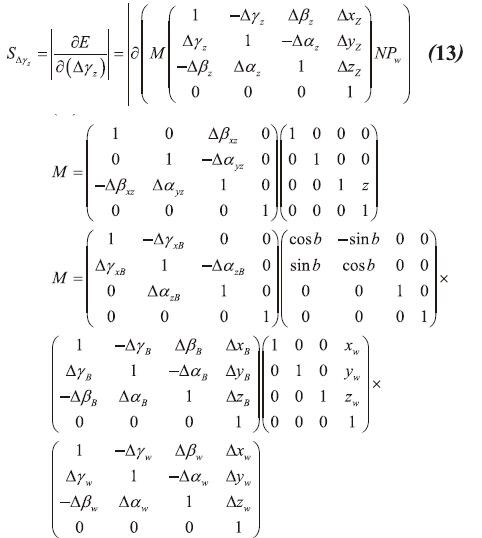
将上面的误差参数值代入到式（13），并进行整理，计算得

进一步可计算得到△γz对应的误差敏感度为

用同样的计算方法，可以计算出精密卧式加工中心的精度模型中各误差元素的敏感度。表6列出了加工中心各误差元素对应的空间误差E的表达式（部分），而从E的表达式中很容易得到相应的Si。

由表4可知，精度模型中的几何误差元素值按表3的数值取，并按试件的加工设定坐标变量后，总误差E与各项误差元素Δei的关系为
E=ai+ki△ei（14）
在分别对Em（m=x,y,z）进行分析时，式（14）中系数ki的绝对值越大，表明误差元素Δei相对应的敏感度Si越大，其对空间误差Em的变化影响也越大。为了更好地识别和分析关键性误差源，将各误差源参数的敏感度系数进行归一化处理，定义

式中，smi为Δei对应的误差敏感度系数，所以敏感度系数之和为1。

对各几何误差对应的敏感度系数进行分析可知，误差敏感度系数越大，表明总误差E对误差元素Δei的变化敏感度越大，也即该几何误差源是影响机床总加工精度的一个关键因素，其对应的机床零部件对机床整机的加工精度影响越大。其中对Ex影响较大的关键性误差源有6项，其对应的误差表达式、敏感度和敏感度系数如表7所示。

表7中，Δγx、Δγz、ΔγB、Δγxy、ΔγxB这几项误差为机床本身的设计误差，Δγw为工件安装时产生的误差。图5a为此六项误差元素对应的误差敏感度系数比较图。从图5中可以看出这6项误差的敏感度系数之和为0.89，其他误差对应的敏感度系数仅为0.11。通过计算分析，可见机床的x轴运动部件、z轴运动部件、工作台B轴转动部件绕z轴的转角误差，x、y轴的垂直度误差，x、B轴的垂直度误差，以及工件安装时绕z轴的转角误差在加工零件时对总的空间误差在x轴方向的误差分量Ex影响较大。

同理，可以识别出对Ey、Ez产生重要影响的关键性误差源参数。如图5b所示，对Ey变化敏感度大的误差元素有Δγz、ΔγB、ΔγxB、Δγw，这4项误差的敏感度系数之和为0.82，其他误差对应的敏感度系数仅为0.18。可见机床的z轴运动部件、工作台B轴转动部件绕z轴的转角误差，x、B轴的垂直度误差，以及工件安装时绕x轴产生的转角误差在机床加工过程中对总的空间误差在y轴方向的误差分量Ey影响较大。

如图5c所示，对Ez变化敏感度大的误差元素，有Δαx、Δαz、ΔαB、Δαw、Δαyz、ΔαzB、Δβz、ΔβB、Δβxz。这9项误差的敏感度系数之和为0.9，其他误差对应的敏感度系数仅为0.1。可知机床的x轴运动部件绕x轴的转角误差，z轴运动部件、工作台B轴转动部件绕x和y轴的转角误差，y、z轴的垂直度误差，x、z轴的垂直度误差，z、B轴的垂直度误差，以及工件安装时绕x轴的转角误差在加工零件时对总的空间误差在z轴方向的误差分量Ez影响较大。

2.4灵敏度分析结果

通过对精密卧式加工中心进行误差灵敏度分析，可以得到以下几点。

（1）机床的z轴运动部件、工作台B轴转动部件绕z轴的转角误差（Δγz：z轴导轨在垂直平面内平行度误差的反映，ΔγB：工作台沿x轴方向的水平度误差的反映），以及x、B轴的垂直度误差ΔγxB等这三项误差对Ex、Ey的变化灵敏度都很大，因此，在机床的精度设计时应重点控制这几个误差的值。

（2）在机床的各个部件中，z轴导轨的直线度和平行度误差、工作台B轴转动部件产生的误差对总的空间误差E产生的影响较大。

（3）影响Ex的主要误差有6项，影响Ey的主要误差有4项，而影响Ez的主要误差有9项。相比较而言，Ez受到的基本误差元素的影响更复杂。

3结论

（1）精度建模与误差敏感度分析是机床精度设计的核心内容之一。用多体系统理论的方法，综合考虑机床各部件的几何误差，建立了精密卧式加工中心的精度模型。

（2）根据精度模型，提出了四轴数控机床的误差敏感度分析方法，用矩阵微分法建立四轴数控机床的敏感度分析模型，并推导出精密卧式加工中心的敏感度分析模型。

（3）以误差检测试验和加工典型标准试件为例对加工中心进行误差敏感度分析，得到z轴导轨在垂直平面内的平行度误差、工作台沿x轴方向的水平度误差以及x、B轴的垂直度误差ΔγxB等这几项误差因素对Ex、Ey的影响较关键，最终识别出了影响机床加工精度的关键性误差，实现了误差溯源，为精密数控机床的设计提供了重要的理论依据。